أسهل شرح للمعادلات على المتجهات للصف الثالث الإعدادي مع أمثلة محلولة
مقدمة
المعادلات على المتجهات تُعد من أهم الدروس في فرع الجبر والهندسة التحليلية، وتظهر كثيرًا في امتحانات الصف الثالث الإعدادي والثانوي. تهدف هذه المعادلات إلى التعامل مع كميات لها مقدار واتجاه، مثل القوة والسرعة. في هذا المقال، نقدم شرحًا مبسطًا وموسوعيًا لطريقة حل المعادلات التي تتضمن متجهات، مع تدريبات محلولة وأمثلة تطبيقية.
أولًا: ما هو المتجه؟
- المتجه: كمية لها مقدار واتجاه، ويرمز له عادة بسهم فوق الحرف: →𝐀 أو \vec{A}.
- يمثل المتجه غالبًا:
- سرعة
- قوة
- إزاحة
الفرق بين الكمية المتجهة والعددية:
| النوع | التعريف | مثال |
|---|---|---|
| كمية عددية (Scalar) | لها مقدار فقط | الكتلة – الزمن |
| كمية متجهة (Vector) | لها مقدار واتجاه | القوة – السرعة |
ثانيًا: كيفية تمثيل المتجهات
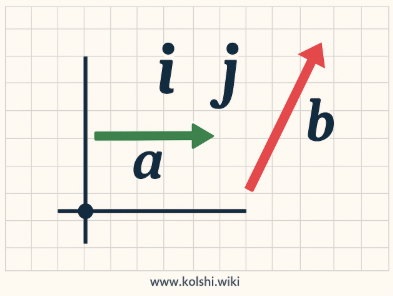
- بيانيًا: باستخدام سهم في الاتجاه المطلوب.
- جبريًا: باستخدام الإحداثيات (مثلاً: 𝐀 = 3𝑖 + 2𝑗)
حيث 𝑖 و 𝑗 هما متجهات الوحدة في الاتجاه الأفقي والرأسي.
ثالثًا: العمليات الأساسية على المتجهات
1. الجمع:
- يتم بجمع المركبات المناظرة:إذا كان 𝐀 = 2𝑖 + 3𝑗، و𝐁 = 4𝑖 + 1𝑗 فإن: 𝐀 + 𝐁 = (2+4)𝑖 + (3+1)𝑗 = 6𝑖 + 4𝑗
2. الطرح:
- يتم بطرح المركبات المناظرة:𝐀 − 𝐁 = (2−4)𝑖 + (3−1)𝑗 = −2𝑖 + 2𝑗
3. الضرب في عدد:
- يُضرب كل مركب في العدد:3𝐀 = 3(2𝑖 + 3𝑗) = 6𝑖 + 9𝑗
رابعًا: المعادلات على المتجهات
يتم فيها حل معادلات تحتوي على متغيرات داخل المتجهات.
مثال 1:
إذا كان 𝐀 = 2𝑖 + 𝑥𝑗، و𝐁 = 2𝑖 + 5𝑗، وكان 𝐀 = 𝐁، أوجد 𝑥.
الحل:
- مساواة المركبات:
- 2𝑖 = 2𝑖 → ✅ صحيحة
- 𝑥𝑗 = 5𝑗 → إذن 𝑥 = 5
مثال 2:
إذا كان 𝐀 = 3𝑖 + 4𝑗، و𝐁 = −1𝑖 + 2𝑗، أوجد 𝐀 + 𝐁.
الحل:
- جمع المركبات:
- 𝑖: 3 + (−1) = 2
- 𝑗: 4 + 2 = 6 → الناتج: 2𝑖 + 6𝑗
خامسًا: تدريبات محلولة
تدريب 1:
إذا كان 𝐀 = 𝑥𝑖 + 2𝑗، و𝐁 = 3𝑖 + 2𝑗، و𝐀 = 𝐁، أوجد 𝑥.
الحل: 𝑥 = 3
تدريب 2:
𝐀 = 4𝑖 + 3𝑗، 𝐁 = 2𝑖 − 𝑗، أوجد: أ. 𝐀 − 𝐁 ب. 2𝐀
أ: (4−2)𝑖 + (3−(−1))𝑗 = 2𝑖 + 4𝑗 ب: 2 × (4𝑖 + 3𝑗) = 8𝑖 + 6𝑗
تدريب 3:
𝐀 = 2𝑖 + 5𝑗، 𝐁 = −3𝑖 + 𝑥𝑗، وكان 𝐀 + 𝐁 = −1𝑖 + 9𝑗. أوجد 𝑥.
الحل:
- 2 + (−3) = −1 → ✅
- 5 + 𝑥 = 9 → إذن 𝑥 = 4
سادسًا: أسئلة امتحانية متوقعة
- إذا كان 𝐀 = 𝑥𝑖 + 2𝑗، و𝐁 = 3𝑖 + 2𝑗، و𝐀 = 𝐁، أوجد 𝑥.
- أوجد 𝐀 + 𝐁 إذا كان: 𝐀 = 4𝑖 − 𝑗، 𝐁 = −2𝑖 + 3𝑗.
- إذا كان: 𝐀 = 2𝑖 + 𝑥𝑗، و𝐁 = 2𝑖 + 5𝑗، وكان 𝐀 = 𝐁، فما قيمة 𝑥؟
خاتمة
فهم المعادلات على المتجهات يُساعد الطالب على إتقان جزء هام من مادة الرياضيات، خصوصًا في الهندسة والفيزياء. بالاعتماد على التدريبات المتكررة وفهم خطوات الحل، يمكن للطالب تحقيق أفضل أداء في هذا الدرس.
المصادر:
- كتاب المدرسة – وزارة التربية والتعليم
- بنك المعرفة المصري
- موقع كورسات رياضيات تعليمية مصرية